Persamaan diferensial, pernyataan matematis yang mengandung satu atau lebih turunan — yaitu, istilah yang mewakili tingkat perubahan dari jumlah yang bervariasi secara terus menerus. Persamaan diferensial sangat umum dalam sains dan teknik, serta di banyak bidang studi kuantitatif lainnya, karena apa yang dapat diamati dan diukur secara langsung untuk sistem yang mengalami perubahan adalah tingkat perubahannya. Solusi dari persamaan diferensial adalah, secara umum, persamaan yang mengekspresikan ketergantungan fungsional dari satu variabel pada satu atau lebih yang lain; biasanya berisi istilah konstan yang tidak ada dalam persamaan diferensial asli. Cara lain untuk mengatakan ini adalah bahwa solusi persamaan diferensial menghasilkan fungsi yang dapat digunakan untuk memprediksi perilaku sistem asli, setidaknya dalam batasan tertentu.

analisis: Newton dan persamaan diferensial
penerapan analisis adalah persamaan diferensial, yang menghubungkan tingkat perubahan berbagai kuantitas dengan nilai saat ini,
Persamaan diferensial dikelompokkan menjadi beberapa kategori besar, dan ini selanjutnya dibagi lagi menjadi banyak subkategori. Kategori yang paling penting adalah persamaan diferensial biasa dan persamaan diferensial parsial. Ketika fungsi yang terlibat dalam persamaan hanya bergantung pada satu variabel tunggal, turunannya adalah turunan biasa dan persamaan diferensial digolongkan sebagai persamaan diferensial biasa. Di sisi lain, jika fungsi tergantung pada beberapa variabel independen, sehingga turunannya adalah turunan parsial, persamaan diferensial dikelompokkan sebagai persamaan diferensial parsial. Berikut ini adalah contoh persamaan diferensial biasa:
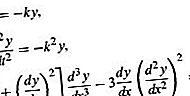
Di sini, y berarti fungsi, dan t atau x adalah variabel independen. Simbol k dan m digunakan di sini untuk menyatakan konstanta tertentu.
Apa pun jenisnya, persamaan diferensial dikatakan sebagai urutan ke-n jika melibatkan turunan dari urutan ke-n tetapi tidak ada turunan dari urutan yang lebih tinggi dari ini. Persamaan ini adalah contoh persamaan diferensial parsial dari orde kedua. Teori-teori persamaan diferensial biasa dan parsial sangat berbeda, dan untuk alasan ini kedua kategori diperlakukan secara terpisah.
Alih-alih persamaan diferensial tunggal, objek penelitian mungkin merupakan sistem simultan dari persamaan tersebut. Perumusan hukum dinamika sering mengarah pada sistem seperti itu. Dalam banyak kasus, persamaan diferensial tunggal urutan ke-n menguntungkan diganti oleh sistem persamaan simultan, yang masing-masingnya adalah urutan pertama, sehingga teknik dari aljabar linier dapat diterapkan.
Persamaan diferensial biasa di mana, misalnya, fungsi dan variabel independen dilambangkan dengan y dan x pada dasarnya merupakan ringkasan implisit dari karakteristik esensial y sebagai fungsi x. Karakteristik ini mungkin akan lebih mudah diakses untuk dianalisis jika formula eksplisit untuk y dapat diproduksi. Rumus seperti itu, atau setidaknya persamaan dalam x dan y (tidak melibatkan turunan) yang dapat dikurangkan dari persamaan diferensial, disebut solusi dari persamaan diferensial. Proses menyimpulkan solusi dari persamaan dengan aplikasi aljabar dan kalkulus disebut memecahkan atau mengintegrasikan persamaan. Perlu dicatat, bagaimanapun, bahwa persamaan diferensial yang dapat diselesaikan secara eksplisit tetapi minoritas kecil. Dengan demikian, sebagian besar fungsi harus dipelajari dengan metode tidak langsung. Bahkan keberadaannya harus dibuktikan ketika tidak ada kemungkinan memproduksinya untuk diperiksa. Dalam praktiknya, metode dari analisis numerik, yang melibatkan komputer, digunakan untuk mendapatkan solusi perkiraan yang berguna.